Tl;dr Cool encoding using Rubik’s cube, I wrote a Python script.

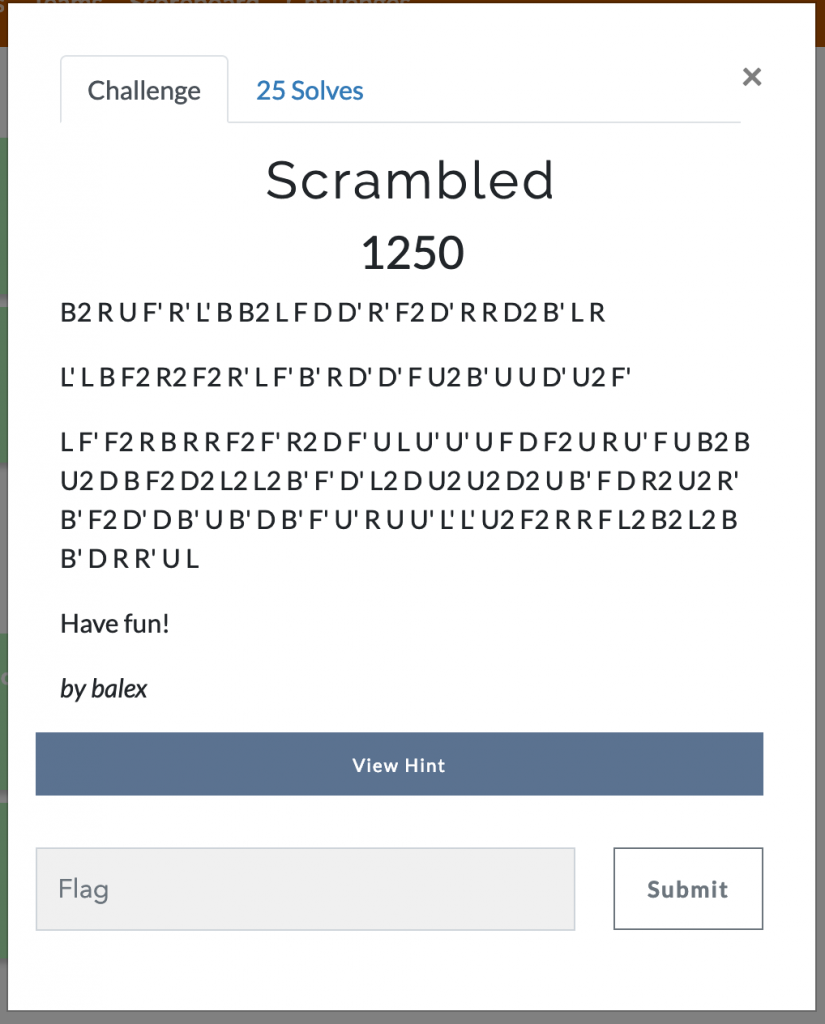
This was a 1250 point Forensics challenge (highest points in the category). Here’s the description:

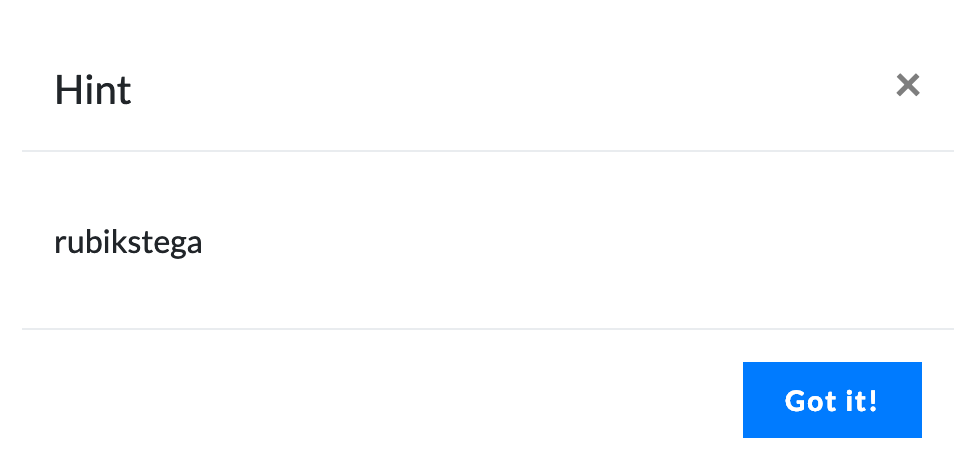
By the time I took a look at the challenge, they had released a hint as well:

Based on the hint, I quickly discovered that the challenge description described ways of manipulating a Rubik’s Cube:

Googling the hint (“rubikstega”) leads to a paper entitled “Rubikstega: A Novel Noiseless Steganography Method in Rubik’s Cube” (link). After skimming through the paper, it became clear that this was the method used to encode the message, so I got reading.

Here’s how the encoding works (at a high level, I’ll break it down more as I go through the challenge):

• Each message has 3+ “scrambles”.
  • The first scramble provides a permutation value
  • The second provides the length of the message
  • The rest of the scrambles make up the message
• The encoding uses base 9 in order to encode messages. Since there are 18 possible moves, there are two moves for each base 9 value:

Let’s take a look at the first scramble. This will eventually yield a permutation value (P) that is used to mutate the default message encoding table for the rest of the scrambles.

B2 R U F’ R’ L’ B B2 L F D D’ R’ F2 D’ R R D2 B’ L R

Scramble 1

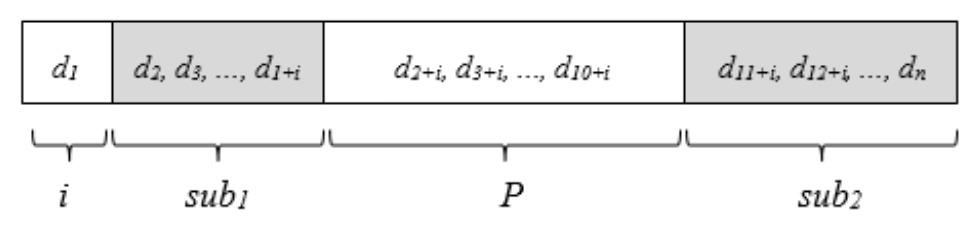
1. First, we translate each move to a Base-9 value using the default encoding table. This gives us:
   • 512676150038748115801
2. Then, we convert that Base-9 value to Base-10. This gives us:
   • 62553673461870258607
3. Now we can extract the permutation value. The first digit (i) is 6, so we skip 6 more digits and then take the next 9. This gives us P:
   • 346187025

Now that we have the permutation value, we can modify the original encoding table for the rest of the scrambles:

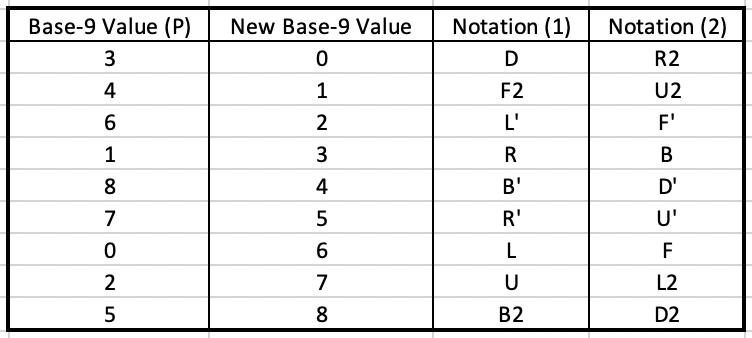
Now we can take a look at scramble 2. This will eventually yield the message length for the rest of the scrambles.

L’ L B F2 R2 F2 R’ L F’ B’ R D’ D’ F U2 B’ U U D’ U2 F’

Scramble 2

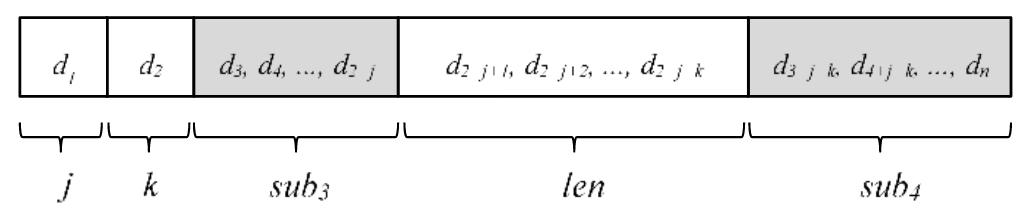
1. First, we translate each move to Base-9 using the new encoding table that we created using P. This gives us:
   • 263101562434461477412
2. Next, we convert that Base-9 value to Base-10. This gives us:
   • 32887738540626863753
3. The first digit is j, and the second digit is k. Therefore:
   • j = 3, and k = 2
4. We get the start of the length by doing:
   • 2+j+1 = 2+3+1 = 6
5. We get the end of the lengthy by doing:
   • 2+j+k = 2+3+2 = 7
6. We take the Base-10 value as a string, and the numbers between indexes 6 and 7 are the length. Therefore:
   • The message length is 73

Now we know we need to take 73 moves from the third scramble to decode our flag.

L F’ F2 R B R R F2 F’ R2 D F’ U L U’ U’ U F D F2 U R U’ F U B2 B U2 D B F2 D2 L2 L2 B’ F’ D’ L2 D U2 U2 D2 U B’ F D R2 U2 R’ B’ F2 D’ D B’ U B’ D B’ F’ U’ R U U’ L’ L’ U2 F2 R R F L2 B2 L2 B B’ D R R’ U L

Scramble 3 (in it’s entirety, ~80 moves)

1. First, we translate each move to Base-9 using the new encoding table again. This gives us:
   • 6213333120027655760173567831031877424701187460015414047404253752211336787
2. Then, you convert that to binary (Base-2). This gives us:
   • 111010101110100011001100110110001100001011001110… (you get the point)
3. Then you pad it with 0s at the beginning so you have equal blocks of 8. I won’t dump all that binary again, but you need one 0 at the beginning.
4. Then, you break it into blocks of 8 and convert to ASCII. This gives us the flag.

At first I did this by hand, but I messed up somewhere and wasn’t able to get the proper ASCII values so I wrote a Python script, which you can see here. Definitely wouldn’t recommend trying to do this by hand.

The flag is utflag{my_bra1n_1s_scrambl3d}.